Physicists at the University of Colorado Boulder have gone to creative lengths to earn their scouting merit badges for knot-tying.
In a study that will appear Sept. 26 in the journal Science, a team of researchers discovered a new way to tie microscopic knots within a solution of liquid crystals. This type of material is found in a wide range of electronics from high-definition TVs to cellphone screens.
And while the tiny knots won’t help you to secure a rowboat or pitch a tent, they are a feat of control, said Jung-Shen (Benny) Tai, lead author of the new research. Once tied, these molecular pretzels won’t untie, and they can come together to form large, three-dimensional crystals.
“By changing the voltage we apply to the liquid crystal with our knots, we can make them expand or shrink and even form the CU Boulder logo when manipulated using lasers,” said Tai, a graduate student in the Department of Physics.
[ad_336]
Co-author Ivan Smalyukh believes that the team’s liquid crystal knots will have other uses, too.
Physicists, he explained, have long been interested in how knots might form in a wide range of physical fields, such as those emerging from magnets. The problem is that these phenomena aren’t easy to observe or manipulate using conventional tools.
“Scientists have proposed knots like these in cosmology, nuclear physics, particle physics, everywhere,” said Smalyukh, a professor of physics. “But what is beautiful about liquid crystals is that you can see and study them under a microscope.”
He added that the study builds on humanity’s long-running obsession with knots. Such shapes have played a central role in the artwork of Celtic, Norse, Tibetan and Chinese cultures, to name a few.
“Humankind has been fascinated by knots for millennia,” Smalyukh said.
Scientists are no exception. In the 19th century, for example, famed physicists William Thomson and James Clerk Maxwell proposed that atoms themselves might be made up of tiny knots of energy. This model was eventually debunked, but it helped to inspire a current area of research called mathematical knot theory.

And it pushed a lot of scientists to look for knots in other physical phenomena. For their part, Smalyukh and Tai turned to liquid crystals.
These types of materials are useful because they behave a little like solids and a little like liquids.
[rand_post]
In the new study, the researchers experimented with a type of liquid crystal molecule that is shaped like a helix, or a small screw. Because those screws don’t fit together well, they tend to twist, Smalyukh said. As a result, if you mix them under just the right conditions, small kinks will begin to appear in the solution. Through a microscope, those kinks look a bit like grains of sand floating in a glass of water.
But they’re not grains. They’re knots.
“We’re seeing a huge number of molecules that know how to tie knots,” Smalyukh said.
Put another way, the molecules within the tiny kinks point in different directions than those around them. And if you measure their collective orientations in different locations, they trace the line of a knot.
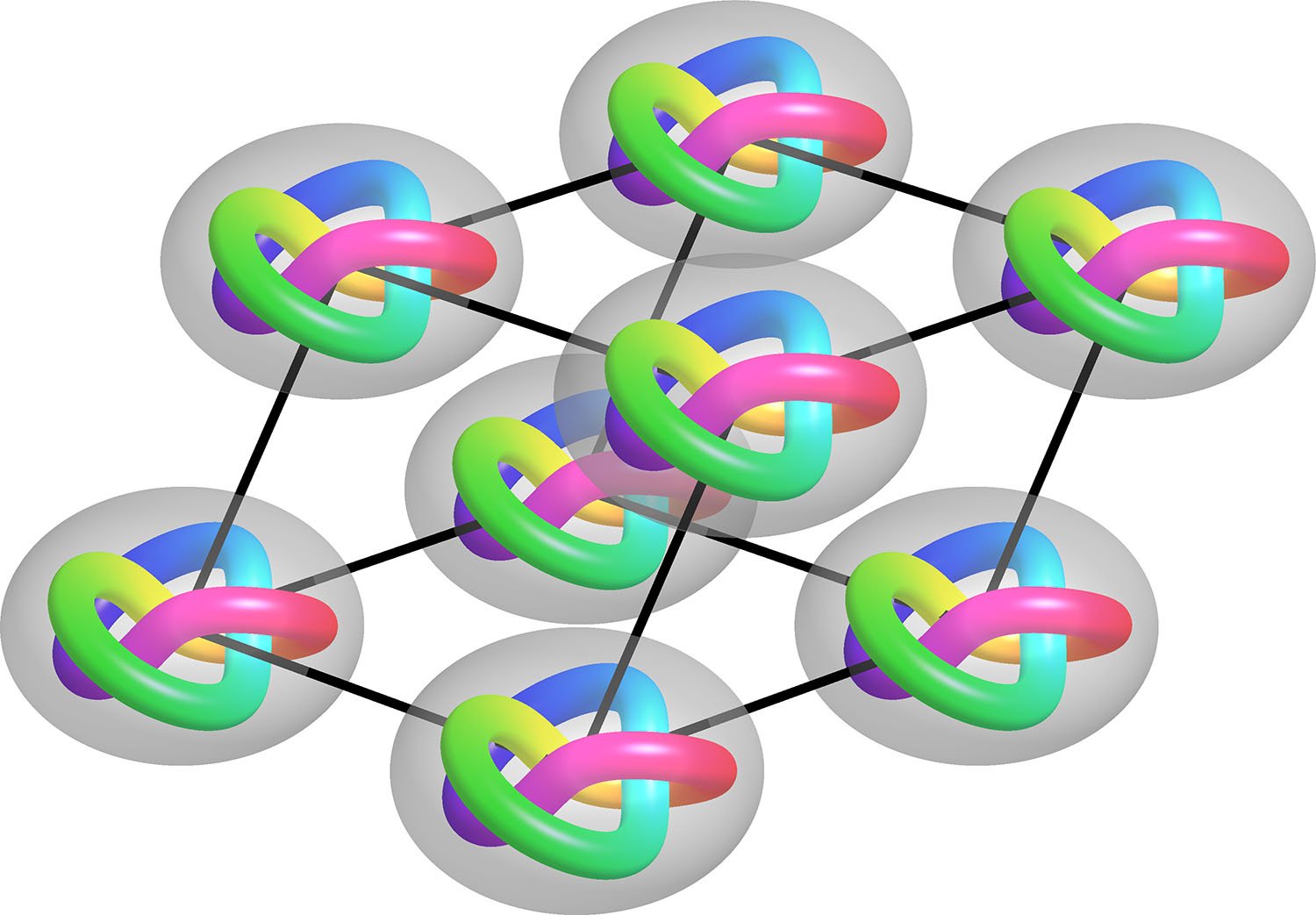
Tai added that the team has seen several different kinds of knots appear in their liquid crystal solutions. The most basic is the trefoil knot, which crosses over itself three times and was a popular motif in Celtic artwork.

“We also had more complicated ones like cinquefoil knots, or knots with five crossings, and even ones with seven crossings,” he said.
[ad_336]
Like the best knots, these creations won’t snap unless the researchers disturb the surrounding medium–the equivalent of using a scissors to snip them. As a result, the team was able to use lasers to move the knots around, nudging them together to form much bigger structures.
“With liquid crystals, we can easily image and analyze these knots and compare them to actual mathematical knots,” Tai said. “So this provides a very nice platform to test knot theory.”
Smalyukh agreed and said that it’s also just exciting to find a new way to play with knots.
“We know that there is a beautiful history of people being fascinated by the possibility of knots in fields,” he said. “But it was quite unexpected to see them in this embodiment right in front of our eyes.”